数据结构之树、二叉树、图的遍历——软件测试工程师面试秘籍
时间: 2021-11-23 13:12 作者: G. li 点击次数:
2.1.3 树、二叉树、图的遍历
考点:
·树的深度优先、广度优先遍历算法
·二叉树先序、中序、后序遍历,满二叉树、完全二叉树的定义
·图的深度优先、广度优先遍历算法
1.树
树的遍历方式有深度优先和广度优先两种。
深度优先搜索就是在树的每一层始终只扩展一个子节点,不断地向下一层前进,直到到达叶子节点或受到深度限制时,才从当前节点返回上一层节点,沿着另一个方向继续前进。广度优先搜索是指深度越小的节点越先得到扩展,本层的节点没有遍历完时,不能对下一层节点进行处理。
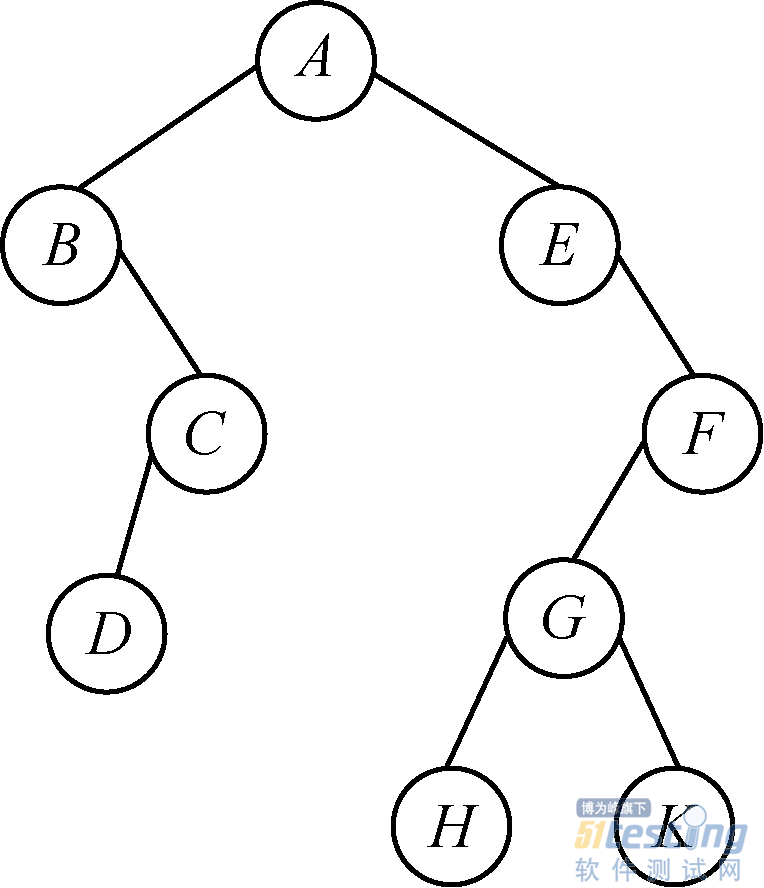
对于图2.8所示的树,深度遍历结果为ABCDEFGHK,广度遍历结果为ABECFDGHK。
图2.8 树
深度优先遍历算法中,采用栈来实现非递归算法。以二叉树为例,代码如下:
public void depthOrderTraversal(){
if(root==null){
System.out.println("empty tree");
return;
}
ArrayDeque<TreeNode> stack=new ArrayDeque<TreeNode>();
stack.push(root);
while(stack.isEmpty()==false){
TreeNode node=stack.pop();
System.out.print(node.value+" ");
if(node.right!=null){
stack.push(node.right);
}
if(node.left!=null){
stack.push(node.left);
}
}
System.out.print("
");
}
广度优先遍历算法利用队列来实现非递归算法。以二叉树为例,代码如下:
public void levelOrderTraversal(){
if(root==null){
System.out.println("empty tree");
return;
}
ArrayDeque<TreeNode> queue=new ArrayDeque<TreeNode>();
queue.add(root);
while(queue.isEmpty()==false){
TreeNode node=queue.remove();
System.out.print(node.value+" ");
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
System.out.print("
");
}
2.二叉树
二叉树是树的一种,它的每个节点最多只有两个子节点,并且左、右子节点次序不能对调。二叉树的5个特性如下。
(1)在二叉树的第i层上至多有2i-1个节点(i≥1)。
(2)深度为k的二叉树上至多含2k-1个节点(k≥1)。
(3)对任何一棵二叉树,若它有n0个叶子节点、n1个度为2的节点,则一定存在关系式n0=n1+1。
(4)具有n个节点的完全二叉树的深度为log2(n+1)。
(5)如果对一棵有n个节点的完全二叉树的节点按层编号,则对任意节点i(1≤i≤n)有如下规律。
① 若i=1,则节点i是二叉树的根;若i>1,则父节点是节点i/2。
② 若2i>n,则节点i无左子节点;否则,左子节点是节点2i。
③ 若2i+1>n,则节点i无右子节点;否则,右子节点是节点2i+1。
二叉树有3种遍历方式—先序遍历、中序遍历和后序遍历。二叉树遍历是笔试中的常见考题。
先序遍历的步骤如下:
(1)访问根节点。
(2)先序遍历左子树。
(3)先序遍历右子树。
中序遍历的步骤如下:
(1)中序遍历左子树。
(2)访问根节点。
(3)中序遍历右子树。
后序遍历的步骤如下:
(1)后序遍历左子树。
(2)后序遍历右子树。
(3)访问根节点。
试题1.写出图2.8所示树的先序、中序和后序遍历结果。
答案如下。
先序遍历结果是ABCDEFGHK。
中序遍历结果是BDCAEHGKF。
后序遍历结果是DCBAHKGFEA。
试题2.根据先序遍历结果ABDCEFGHK、中序遍历结果BDCAEHGKF,写出后序遍历结果。
分析如下。
(1)根据先序遍历结果可以得到整个树的根节点是A。
(2)从中序遍历结果得到A左边的BDC是左子树,EHGKF是右子树。
(3)以BDC作为左子树先序遍历结果,说明B是子树的根;又由于中序遍历结果为BDC,说明DC是在B的右子树上。
(4)先序遍历结果和中序遍历结果一样,说明根为D,C是D的右子树。
(5)回到A的右子树EHGKF这几个节点,先序遍历结果为E,右子树根为E。
(6)中序遍历结果为EHGKF,说明HGKF在E的右子树。
(7)HGKF的先序遍历结果为FGHK,则F为根节点;中序遍历结果为HGKF,则HGK为F的左子树。
(8)HGK的先序遍历结果为GHK,则G为根节点;中序遍历结果为HGK,则H为左子树,K为右子树。这样把树形结构还原之后,后序遍历结果为DCBAHKGFEA。
满二叉树和完全二叉树的定义如下。
满二叉树:一棵深度为k,且有2k-1个节点的二叉树,每一层上的节点数都是最大节点数。
完全二叉树:深度为k,有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1至n的节点一一对应时,称为完全二叉树。叶子节点只可能在层次最大的两层上出现;对于任意节点,若其右子树下子孙节点的最大层次为l,则其左子树下子孙节点的最大层次必为l或l+1。
3.图
图的遍历是指从图中的任意顶点出发,对图中的所有顶点访问一次且只访问一次。
图的遍历目前有深度优先搜索法和广度(宽度)优先搜索法两种算法。
深度优先搜索法是树的先序遍历的推广,它的基本思想是从图G的某个顶点v0出发,访问v0,然后选择一个与v0相邻且没被访问过的顶点vi并访问,再从vi出发选择一个与vi相邻且未被访问的顶点vj并访问,依此类推。如果当前被访问过的顶点的所有相邻顶点都已被访问,则退回已被访问的顶点序列中最后一个拥有未被访问的相邻的顶点w,从w出发按同样的方法向前遍历,直到图中所有顶点都被访问。其递归算法如下。
Boolean visited[MAX_VERTEX_NUM]; //访问标志数组
Status (*VisitFunc)(int v); //VisitFunc()是访问函数,对图的每个顶点调用该函数
void DFSTraverse(Graph G,Status(*Visit)(int v)){
VisitFunc=Visit;
for(v=0;v<G.vexnum;++v)
visited[v]=FALSE; //访问标志数组初始化
for(v=0;v<G.vexnum;++v)
if(!visited[v])
DFS(G,v); //对尚未访问的顶点调用DFS()函数
}
void DFS(Graph G,int v){ //从v出发递归地深度优先遍历图
visited[v]=TRUE; VisitFunc(v); //访问v
for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))
//FirstAdjVex()返回v的第1个相邻顶点,若顶点在图中没有相邻顶点,则返回0
//若w是v的相邻顶点,NextAdjVex()返回v的(相对于w的)下一个相邻顶点
//若w是v的最后一个相邻顶点,则返回0
if(!visited[w])
DFS(G, w); //对v的尚未访问的相邻顶点w调用DFS()函数
}
图的广度优先搜索法是树的按层次遍历的推广,它的基本思想是首先访问初始点vi,并将其标记为已访问,然后访问vi的所有未被访问的相邻顶点vi1,vi2,…,vit,并均标记已访问,接着按照vi1,vi2,…,vit的次序,访问每一个顶点的所有未被访问的相邻顶点,并均标记为已访问。以此类推,直到图中所有和初始点vi有路径相通的顶点都被访问为止。其非递归算法如下:
Boolean visited[MAX_VERTEX_NUM]; //访问标志数组
Status (*VisitFunc)(int v); //VisitFunc()是访问函数,对图的每个顶点调用该函数
void BFSTraverse (Graph G, Status(*Visit)(int v)){
VisitFunc=Visit;
for(v=0;v<G.vexnum,++v)
visited[v]=FALSE;
initQueue(Q); //置空辅助队列Q
for(v=0;v<G.vexnum;++v)
if(!visited[v]){
visited[v]=TRUE; VisitFunc(v);
EnQueue(Q,v); //v入列
while(!QueueEmpty(Q)){
DeQueue(Q, u); //队头元素出队并设置为u
for(w=FirstAdjVex(G,u);w>=0;w=NextAdjVex(G,u,w))
if(!Visited[w]){ //w为u的尚未访问的相邻顶点
Visited[w]=TRUE;VisitFunc(w);
EnQueue(Q, w);
}
}
}
}
打印本页 | 加入收藏
上一篇:测试岗位真的会被开发取代么? 下一篇:【51讲堂】手机端自动化测试
文章检索
热门关键词: 登录